310. Minimum Height Trees #117
-
|
Topics: A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree. Given a tree of Return a list of all MHTs' root labels. You can return the answer in any order. The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf. Example 1:
Example 2:
Constraints:
Hint:
|
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We can use the concept of graph theory to find nodes that, when chosen as roots, minimize the height of the tree. The basic idea is to perform a two-pass Breadth-First Search (BFS) to find these nodes efficiently. Steps to Solve the Problem
Let's implement this solution in PHP: 310. Minimum Height Trees <?php
/**
* @param Integer $n
* @param Integer[][] $edges
* @return Integer[]
*/
function findMinHeightTrees($n, $edges) {
if ($n == 1 || empty($edges)) {
return [0];
}
$ans = [];
$graph = [];
// Build the adjacency list
foreach ($edges as $edge) {
$u = $edge[0];
$v = $edge[1];
$graph[$u][] = $v;
$graph[$v][] = $u;
}
// Initialize leaves
foreach ($graph as $label => $children) {
if (count($children) == 1) {
$ans[] = $label;
}
}
// Remove leaves layer by layer
while ($n > 2) {
$n -= count($ans);
$nextLeaves = [];
foreach ($ans as $leaf) {
$u = current($graph[$leaf]); // There is only one neighbor since it's a leaf
// Remove the leaf from its neighbor's adjacency list
unset($graph[$u][array_search($leaf, $graph[$u])]);
// If neighbor becomes a leaf, add it to newLeaves
if (count($graph[$u]) == 1) {
$nextLeaves[] = $u;
}
}
$ans = $nextLeaves;
}
return $ans;
}
// Example usage:
$n1 = 4;
$edges1 = [[1,0],[1,2],[1,3]];
print_r(findMinHeightTrees($n1, $edges1)); // Output: [1]
$n2 = 6;
$edges2 = [[3,0],[3,1],[3,2],[3,4],[5,4]];
print_r(findMinHeightTrees($n2, $edges2)); // Output: [3,4]
?>Explanation:
This solution efficiently computes the minimum height trees in O(n) time complexity, which is suitable for large values of |
Beta Was this translation helpful? Give feedback.
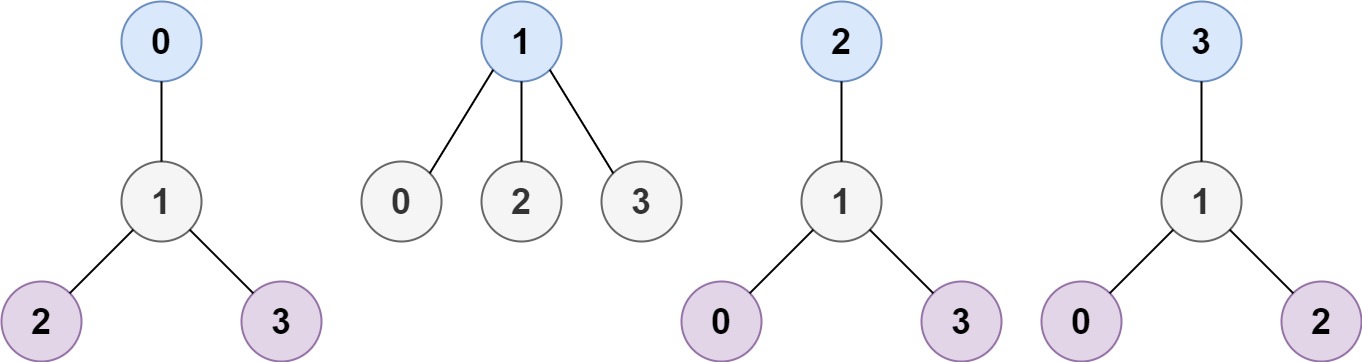
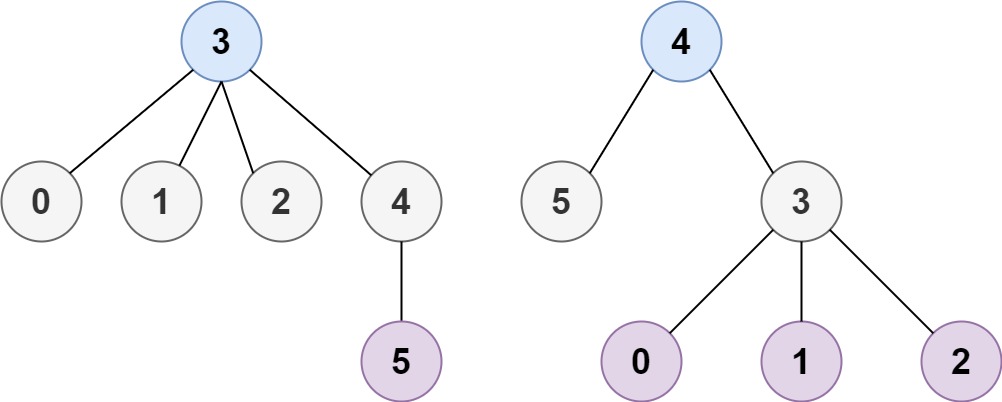
We can use the concept of graph theory to find nodes that, when chosen as roots, minimize the height of the tree. The basic idea is to perform a two-pass Breadth-First Search (BFS) to find these nodes efficiently.
Steps to Solve the Problem
Build the Graph: Represent the tree using an adjacency list. Each node will have a list of its connected nodes.
Find the Leaf Nodes: Leaf nodes are nodes with only one connection.
Trim the Leaves: Iteratively remove the leaf nodes and their corresponding edges from the graph until only one or two nodes remain. These remaining nodes are the potential roots for the minimum height trees.
Return the Result: The remaining nodes after trimming are th…