2493. Divide Nodes Into the Maximum Number of Groups

[mah-shamim]

Topics: Breadth-First Search, Union Find, Graph

You are given a positive integer n representing the number of nodes in an undirected graph. The nodes are labeled from 1 to n.

You are also given a 2D integer array edges, where edges[i] = [ai, bi] indicates that there is a bidirectional edge between nodes ai and bi. Notice that the given graph may be disconnected.

Divide the nodes of the graph into m groups (1-indexed) such that:

• Each node in the graph belongs to exactly one group.
• For every pair of nodes in the graph that are connected by an edge [ai, bi], if ai belongs to the group with index x, and bi belongs to the group with index y, then |y - x| = 1.

Return the maximum number of groups (i.e., maximum m) into which you can divide the nodes. Return -1 if it is impossible to group the nodes with the given conditions.

Example 1:

• Input: n = 6, edges = [[1,2],[1,4],[1,5],[2,6],[2,3],[4,6]]
• Output: 4
• Explanation: As shown in the image we:
  • Add node 5 to the first group.
  • Add node 1 to the second group.
  • Add nodes 2 and 4 to the third group.
  • Add nodes 3 and 6 to the fourth group.
    We can see that every edge is satisfied.
    It can be shown that that if we create a fifth group and move any node from the third or fourth group to it, at least on of the edges will not be satisfied.

Example 2:

• Input: n = 3, edges = [[1,2],[2,3],[3,1]]
• Output: -1
• Explanation: If we add node 1 to the first group, node 2 to the second group, and node 3 to the third group to satisfy the first two edges, we can see that the third edge will not be satisfied.
  It can be shown that no grouping is possible.

Constraints:

• 1 <= n <= 500
• 1 <= edges.length <= 104
• edges[i].length == 2
• 1 <= ai, bi <= n
• ai != bi
• There is at most one edge between any pair of vertices.

Hint:

1. If the graph is not bipartite, it is not possible to group the nodes.
2. Notice that we can solve the problem for each connected component independently, and the final answer will be just the sum of the maximum number of groups in each component.
3. Finally, to solve the problem for each connected component, we can notice that if for some node v we fix its position to be in the leftmost group, then we can also evaluate the position of every other node. That position is the depth of the node in a bfs tree after rooting at node v.

[mah-shamim]

The problem, "Divide Nodes Into the Maximum Number of Groups", involves determining the maximum number of groups into which the nodes of an undirected graph can be divided, such that:

1. Each node belongs to exactly one group.
2. Adjacent nodes are in groups whose indices differ by exactly 1.
   If the graph is not bipartite, grouping is impossible, and the function must return -1.

Key Points

• Graph Properties: The graph may be disconnected.
• Validation: For each connected component, check if it is bipartite. If not, return -1.
• Bipartite Nature: The solution involves BFS to validate bipartiteness.
• Union-Find: Useful for grouping connected components efficiently.

Approach

1. Preprocessing:

   • Represent the graph using an adjacency list.
   • Use Union-Find to identify connected components.

2. BFS to Validate Bipartiteness:

   • For each connected component, use BFS to determine if it is bipartite.
   • If it is not bipartite, return -1.

3. Calculate Group Count:

   • For each connected component, use BFS to determine the maximum depth, representing the maximum number of groups.

4. Combine Results:

   • Sum the maximum group counts of all bipartite components.

Plan

1. Construct the graph as an adjacency list.
2. Use Union-Find to group connected components.
3. For each node in the graph:
   • Use BFS to check if the graph is bipartite and calculate the maximum depth of that component.
4. Return the sum of the depths of all components as the result. If any component is not bipartite, return -1.

Let's implement this solution in PHP: 2493. Divide Nodes Into the Maximum Number of Groups

<?php
/**
 * @param Integer $n
 * @param Integer[][] $edges
 * @return Integer
 */
function magnificentSets($n, $edges) {
    $graph = array_fill(0, $n, []);
    $uf = new UnionFind($n);
    $rootToGroupSize = [];

    foreach ($edges as $edge) {
        $u = $edge[0] - 1;
        $v = $edge[1] - 1;
        $graph[$u][] = $v;
        $graph[$v][] = $u;
        $uf->unionByRank($u, $v);
    }

    for ($i = 0; $i < $n; $i++) {
        $newGroupSize = $this->bfs($graph, $i);
        if ($newGroupSize == -1) {
            return -1;
        }
        $root = $uf->find($i);
        if (!isset($rootToGroupSize[$root])) {
            $rootToGroupSize[$root] = 0;
        }
        $rootToGroupSize[$root] = max($rootToGroupSize[$root], $newGroupSize);
    }

    $ans = 0;
    foreach ($rootToGroupSize as $groupSize) {
        $ans += $groupSize;
    }

    return $ans;
}

/**
 * @param $graph
 * @param $u
 * @return int
 */
private function bfs($graph, $u) {
    $step = 0;
    $queue = [$u];
    $nodeToStep = [$u => 1];

    while (!empty($queue)) {
        $step++;
        $size = count($queue);
        for ($sz = 0; $sz < $size; $sz++) {
            $current = array_shift($queue);
            foreach ($graph[$current] as $v) {
                if (!isset($nodeToStep[$v])) {
                    $queue[] = $v;
                    $nodeToStep[$v] = $step + 1;
                } elseif ($nodeToStep[$v] == $step) {
                    // There is an odd number of edges in the cycle.
                    return -1;
                }
            }
        }
    }

    return $step;
}

class UnionFind {
    /**
     * @var array
     */
    private $id;
    /**
     * @var array
     */
    private $rank;

    /**
     * @param $n
     */
    public function __construct($n) {
        $this->id = range(0, $n - 1);
        $this->rank = array_fill(0, $n, 0);
    }

    /**
     * @param $u
     * @param $v
     * @return void
     */
    public function unionByRank($u, $v) {
        $i = $this->find($u);
        $j = $this->find($v);
        if ($i == $j) {
            return;
        }
        if ($this->rank[$i] < $this->rank[$j]) {
            $this->id[$i] = $j;
        } elseif ($this->rank[$i] > $this->rank[$j]) {
            $this->id[$j] = $i;
        } else {
            $this->id[$i] = $j;
            $this->rank[$j]++;
        }
    }

    /**
     * @param $u
     * @return mixed
     */
    public function find($u) {
        if ($this->id[$u] == $u) {
            return $u;
        }
        return $this->id[$u] = $this->find($this->id[$u]);
    }
}


// Example usage:
$n = 6;
$edges = [[1,2], [1,4], [1,5], [2,6], [2,3], [4,6]];
echo maxGroups($n, $edges); // Output: 4

$n = 3;
$edges = [[1,2], [2,3], [3,1]];
echo maxGroups($n, $edges); // Output: -1
?>

Explanation:

1. Union-Find Class

The Union-Find (Disjoint Set Union) structure groups nodes into connected components and performs two main tasks:

• Find: Identify the root of a node's connected component.
• Union: Merge two connected components based on rank.

2. BFS for Bipartite Check and Depth Calculation

• Bipartite Validation: Using BFS, assign alternating "colors" to nodes. If adjacent nodes share the same color, the graph is not bipartite.
• Depth Calculation: Measure the depth of the BFS tree to determine the maximum number of groups.

3. Combine Results

• Calculate the maximum depth for each connected component.
• Add the depths for all components to determine the result.

Example Walkthrough

Example 1

Input:

$n = 6;  
$edges = [[1,2], [1,4], [1,5], [2,6], [2,3], [4,6]];

Steps:

1. Construct adjacency list:

   1 -> [2, 4, 5]
   2 -> [1, 3, 6]
   3 -> [2]
   4 -> [1, 6]
   5 -> [1]
   6 -> [2, 4]
   

2. Use BFS on connected components:
   • Component 1: Bipartite. Max depth = 4.
3. Sum depths across all components: 4.

Output: 4

Example 2

Input:

$n = 3;  
$edges = [[1,2], [2,3], [3,1]];

Steps:

1. Construct adjacency list:

   1 -> [2, 3]
   2 -> [1, 3]
   3 -> [1, 2]
   

2. Use BFS:
   • Component 1: Not bipartite.

Output: -1

Time Complexity

• Graph Construction: O(E), where E is the number of edges.
• Union-Find: O(α(N)), where N is the number of nodes (almost constant due to path compression).
• BFS: O(V + E), where V is the number of vertices.
  Overall Complexity: O(N + E)

Output for Examples

$n = 6;
$edges = [[1,2], [1,4], [1,5], [2,6], [2,3], [4,6]];
echo magnificentSets($n, $edges); // Output: 4

$n = 3;
$edges = [[1,2], [2,3], [3,1]];
echo magnificentSets($n, $edges); // Output: -1

This approach efficiently handles the grouping problem by leveraging BFS for bipartiteness checks and depth calculations while utilizing Union-Find to simplify component management. The solution handles both connected and disconnected graphs.

[basharul-siddike]

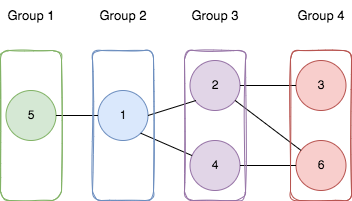
Thanks for solving the problem of "Divide Nodes Into the Maximum Number of Groups"

[mah-shamim]

Thanks