3108. Minimum Cost Walk in Weighted Graph #1456
Answered
by
mah-shamim
mah-shamim
asked this question in
Q&A
-
Beta Was this translation helpful? Give feedback.
Answered by
mah-shamim
Mar 20, 2025
Replies: 1 comment 2 replies
-
|
We need to determine the minimum cost of a walk between two nodes in a weighted undirected graph, where the cost is defined as the bitwise AND of the weights of all edges traversed during the walk. If no such walk exists, the answer should be -1. Approach
Let's implement this solution in PHP: 3108. Minimum Cost Walk in Weighted Graph <?php
class DSU {
/**
* @var array
*/
private $parent;
/**
* @var array
*/
private $rank;
/**
* @param $n
*/
public function __construct($n) {
$this->parent = array();
$this->rank = array();
for ($i = 0; $i < $n; $i++) {
$this->parent[$i] = $i;
$this->rank[$i] = 0;
}
}
/**
* @param $x
* @return mixed
*/
public function find($x) {
if ($this->parent[$x] != $x) {
$this->parent[$x] = $this->find($this->parent[$x]);
}
return $this->parent[$x];
}
/**
* @param $x
* @param $y
* @return bool
*/
public function union($x, $y) {
$xr = $this->find($x);
$yr = $this->find($y);
if ($xr == $yr) {
return false;
}
if ($this->rank[$xr] < $this->rank[$yr]) {
$this->parent[$xr] = $yr;
} else {
$this->parent[$yr] = $xr;
if ($this->rank[$xr] == $this->rank[$yr]) {
$this->rank[$xr]++;
}
}
return true;
}
}
/**
* @param Integer $n
* @param Integer[][] $edges
* @param Integer[][] $query
* @return Integer[]
*/
function minimumCost($n, $edges, $query) {
$dsu = new DSU($n);
foreach ($edges as $edge) {
$dsu->union($edge[0], $edge[1]);
}
$component_and = array_fill(0, $n, -1);
foreach ($edges as $edge) {
$u = $edge[0];
$w = $edge[2];
$root = $dsu->find($u);
$component_and[$root] &= $w;
}
$answer = array();
foreach ($query as $q) {
$s = $q[0];
$t = $q[1];
if ($dsu->find($s) != $dsu->find($t)) {
array_push($answer, -1);
} else {
$root = $dsu->find($s);
array_push($answer, $component_and[$root]);
}
}
return $answer;
}
// Example usage:
$n = 5;
$edges = [[0,1,7],[1,3,7],[1,2,1]];
$query = [[0,3],[3,4]];
print_r(minimumCost($n, $edges, $query)); // Output: [1,-1]
$n = 3;
$edges = [[0,2,7],[0,1,15],[1,2,6],[1,2,1]];
$query = [[1,2]];
print_r(minimumCost($n, $edges, $query)); // Output: [0]
?>Explanation:
This approach efficiently handles the problem constraints using union-find for connectivity and bitwise operations to determine the minimum path cost. |
Beta Was this translation helpful? Give feedback.
2 replies
Answer selected by
kovatz
Sign up for free
to join this conversation on GitHub.
Already have an account?
Sign in to comment
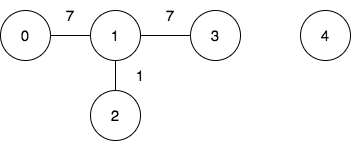
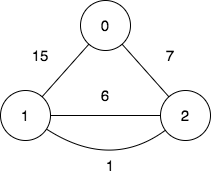
We need to determine the minimum cost of a walk between two nodes in a weighted undirected graph, where the cost is defined as the bitwise AND of the weights of all edges traversed during the walk. If no such walk exists, the answer should be -1.
Approach