1007. Minimum Domino Rotations For Equal Row #1638
-
|
Topics: In a row of dominoes, We may rotate the Return the minimum number of rotations so that all the values in If it cannot be done, return Example 1:
Example 2:
Constraints:
|
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We need to determine the minimum number of rotations required to make all values in either the top row or the bottom row of a set of dominoes the same. If it is not possible, we should return -1. Approach
Let's implement this solution in PHP: 1007. Minimum Domino Rotations For Equal Row <?php
/**
* @param Integer[] $tops
* @param Integer[] $bottoms
* @return Integer
*/
function minDominoRotations($tops, $bottoms) {
$n = count($tops);
$candidates = array($tops[0], $bottoms[0]);
$candidates = array_unique($candidates);
$min_rotations = PHP_INT_MAX;
foreach ($candidates as $x) {
$valid = true;
$rot_top = 0;
$rot_bottom = 0;
for ($i = 0; $i < $n; $i++) {
$t = $tops[$i];
$b = $bottoms[$i];
if ($t != $x && $b != $x) {
$valid = false;
break;
}
if ($t != $x) {
$rot_top++;
}
if ($b != $x) {
$rot_bottom++;
}
}
if ($valid) {
$current_min = min($rot_top, $rot_bottom);
if ($current_min < $min_rotations) {
$min_rotations = $current_min;
}
}
}
return $min_rotations != PHP_INT_MAX ? $min_rotations : -1;
}
// Example 1:
$tops1 = [2,1,2,4,2,2];
$bottoms1 = [5,2,6,2,3,2];
echo minDominoRotations($tops1, $bottoms1) . "\n"; // Output: 2
// Example 2:
$tops2 = [3,5,1,2,3];
$bottoms2 = [3,6,3,3,4];
echo minDominoRotations($tops2, $bottoms2) . "\n"; // Output: -1
?>Explanation:
This approach efficiently narrows down the possible target values and checks each one in linear time, resulting in an overall time complexity of O(n), where n is the number of dominoes. |
Beta Was this translation helpful? Give feedback.
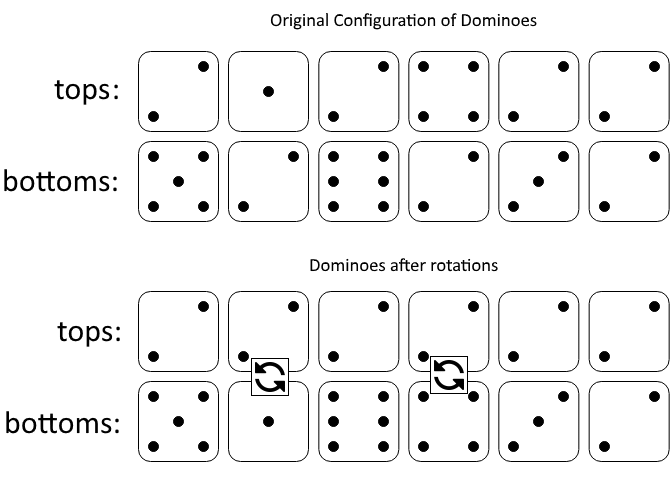
We need to determine the minimum number of rotations required to make all values in either the top row or the bottom row of a set of dominoes the same. If it is not possible, we should return -1.
Approach