3373. Maximize the Number of Target Nodes After Connecting Trees II #1742
-
|
Topics: There exist two undirected trees with You are given two 2D integer arrays Node Return an array of Note that queries are independent from each other. That is, for every query you will remove the added edge before proceeding to the next query. Example 1:
Example 2:
Constraints:
Hint:
|
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We need to maximize the number of target nodes for each node in the first tree after connecting it to any node in the second tree. A node is considered a target to another node if the path between them has an even number of edges. Approach
Let's implement this solution in PHP: 3373. Maximize the Number of Target Nodes After Connecting Trees II <?php
/**
* @param Integer[][] $edges1
* @param Integer[][] $edges2
* @return Integer[]
*/
function maxTargetNodes($edges1, $edges2) {
$n = count($edges1) + 1;
$m = count($edges2) + 1;
$graph2 = array_fill(0, $m, array());
foreach ($edges2 as $edge) {
$u = $edge[0];
$v = $edge[1];
$graph2[$u][] = $v;
$graph2[$v][] = $u;
}
$color2 = array_fill(0, $m, -1);
$color2[0] = 0;
$count0 = 1;
$count1 = 0;
$queue = new SplQueue();
$queue->enqueue(0);
while (!$queue->isEmpty()) {
$node = $queue->dequeue();
foreach ($graph2[$node] as $neighbor) {
if ($color2[$neighbor] == -1) {
$color2[$neighbor] = 1 - $color2[$node];
if ($color2[$neighbor] == 0) {
$count0++;
} else {
$count1++;
}
$queue->enqueue($neighbor);
}
}
}
$base = max($count0, $count1);
$graph1 = array_fill(0, $n, array());
foreach ($edges1 as $edge) {
$u = $edge[0];
$v = $edge[1];
$graph1[$u][] = $v;
$graph1[$v][] = $u;
}
$color1 = array_fill(0, $n, -1);
$color1[0] = 0;
$cnt0 = 1;
$cnt1 = 0;
$queue = new SplQueue();
$queue->enqueue(0);
while (!$queue->isEmpty()) {
$node = $queue->dequeue();
foreach ($graph1[$node] as $neighbor) {
if ($color1[$neighbor] == -1) {
$color1[$neighbor] = 1 - $color1[$node];
if ($color1[$neighbor] == 0) {
$cnt0++;
} else {
$cnt1++;
}
$queue->enqueue($neighbor);
}
}
}
$ans = array();
for ($i = 0; $i < $n; $i++) {
if ($color1[$i] == 0) {
$ans[] = $cnt0 + $base;
} else {
$ans[] = $cnt1 + $base;
}
}
return $ans;
}
// === Test ===
$edges1 = [[0,1],[0,2],[2,3],[2,4]];
$edges2 = [[0,1],[0,2],[0,3],[2,7],[1,4],[4,5],[4,6]];
print_r(maxTargetNodes($edges1, $edges2)); // Expected: [8,7,7,8,8]
$edges1 = [[0,1],[0,2],[0,3],[0,4]];
$edges2 = [[0,1],[1,2],[2,3]];
print_r(maxTargetNodes($edges1, $edges2)); // Expected: [3,6,6,6,6]
?>Explanation:
This approach efficiently leverages bipartite properties of trees to compute the solution in linear time relative to the number of nodes and edges. |
Beta Was this translation helpful? Give feedback.
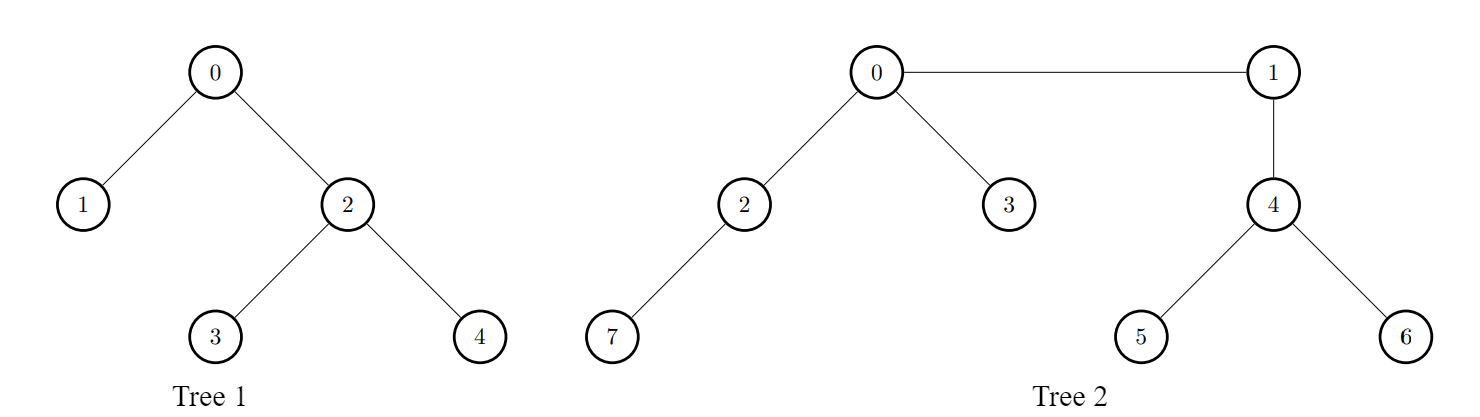
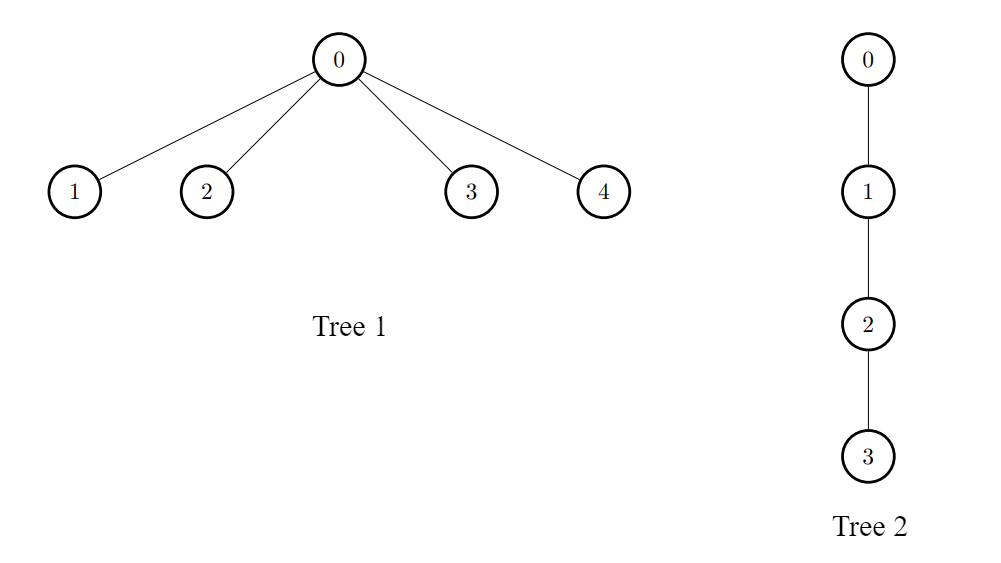
We need to maximize the number of target nodes for each node in the first tree after connecting it to any node in the second tree. A node is considered a target to another node if the path between them has an even number of edges.
Approach
Problem Analysis:
uis a target to nodevif the number of edges on the path fromutovis even. This includes the node itself (distance 0).iin the first tree, we connect it to some nodejin the second tree. The goal is to choosejsuch that the number of target nodes foriis maximized.Key Insight: