1579. Remove Max Number of Edges to Keep Graph Fully Traversable #289
-
|
Topics: Alice and Bob have an undirected graph of
Given an array Return the maximum number of edges you can remove, or return Example 1:
Example 2:
Example 3:
Constraints:
Hint:
|
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We need to find the maximum number of edges that can be removed from an undirected graph such that the graph remains fully traversable by both Alice and Bob. The graph consists of three types of edges: type 1 (Alice only), type 2 (Bob only), and type 3 (both Alice and Bob). The solution involves using Union-Find (Disjoint Set Union, DSU) data structures to efficiently manage and check connectivity for both Alice and Bob. Approach
Let's implement this solution in PHP: 1579. Remove Max Number of Edges to Keep Graph Fully Traversable <?php
class UnionFind {
private $parent;
private $rank;
public function __construct($n) {
$this->parent = range(0, $n);
$this->rank = array_fill(0, $n + 1, 1);
}
public function find($x) {
if ($this->parent[$x] !== $x) {
$this->parent[$x] = $this->find($this->parent[$x]);
}
return $this->parent[$x];
}
public function union($x, $y) {
$rootX = $this->find($x);
$rootY = $this->find($y);
if ($rootX === $rootY) {
return false;
}
if ($this->rank[$rootX] > $this->rank[$rootY]) {
$this->parent[$rootY] = $rootX;
} elseif ($this->rank[$rootX] < $this->rank[$rootY]) {
$this->parent[$rootX] = $rootY;
} else {
$this->parent[$rootY] = $rootX;
$this->rank[$rootX]++;
}
return true;
}
}
/**
* @param Integer $n
* @param Integer[][] $edges
* @return Integer
*/
function maxNumEdgesToRemove($n, $edges) {
// Create two union-find instances for Alice and Bob
$ufAlice = new UnionFind($n);
$ufBob = new UnionFind($n);
// Sort edges by type in descending order to prioritize type 3 edges
usort($edges, function($a, $b) {
return $b[0] - $a[0];
});
$requiredEdges = 0;
foreach ($edges as $edge) {
$type = $edge[0];
$u = $edge[1];
$v = $edge[2];
if ($type === 3) {
$unionAlice = $ufAlice->union($u, $v);
$unionBob = $ufBob->union($u, $v);
if ($unionAlice || $unionBob) {
$requiredEdges++;
}
} elseif ($type === 1) {
if ($ufAlice->union($u, $v)) {
$requiredEdges++;
}
} elseif ($type === 2) {
if ($ufBob->union($u, $v)) {
$requiredEdges++;
}
}
}
// Check if both Alice and Bob can traverse the entire graph
for ($i = 2; $i <= $n; $i++) {
if ($ufAlice->find($i) !== $ufAlice->find(1) || $ufBob->find($i) !== $ufBob->find(1)) {
return -1;
}
}
return count($edges) - $requiredEdges;
}
// Example usage:
$n = 4;
$edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]];
echo maxNumEdgesToRemove($n, $edges); // Output: 2
$n = 4;
$edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]];
echo maxNumEdgesToRemove($n, $edges); // Output: 0
$n = 4;
$edges = [[3,2,3],[1,1,2],[2,3,4]];
echo maxNumEdgesToRemove($n, $edges); // Output: -1
?>Explanation:
This approach efficiently ensures the graph remains traversable for both users while maximizing the number of edges removed. |
Beta Was this translation helpful? Give feedback.
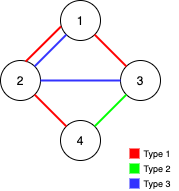
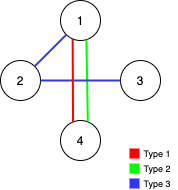
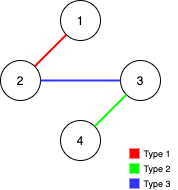
We need to find the maximum number of edges that can be removed from an undirected graph such that the graph remains fully traversable by both Alice and Bob. The graph consists of three types of edges: type 1 (Alice only), type 2 (Bob only), and type 3 (both Alice and Bob). The solution involves using Union-Find (Disjoint Set Union, DSU) data structures to efficiently manage and check connectivity for both Alice and Bob.
Approach
Problem Analysis: The problem requires us to ensure that after removing some edges, both Alice and Bob can traverse the entire graph. This means the graph must remain connected for both Alice (using type 1 and type 3 edges) and Bob (using type 2 and type 3 edge…