1334. Find the City With the Smallest Number of Neighbors at a Threshold Distance

[mah-shamim]

There are n cities numbered from 0 to n-1. Given the array edges where edges[i] = [fromi, toi, weighti] represents a bidirectional and weighted edge between cities fromi and toi, and given the integer distanceThreshold.

Return the city with the smallest number of cities that are reachable through some path and whose distance is at most distanceThreshold, If there are multiple such cities, return the city with the greatest number.

Notice that the distance of a path connecting cities i and j is equal to the sum of the edges' weights along that path.

Example 1:

• Input: n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
• Output: 3
• Explanation: The figure above describes the graph.
  The neighboring cities at a distanceThreshold = 4 for each city are:
  City 0 -> [City 1, City 2]
  City 1 -> [City 0, City 2, City 3]
  City 2 -> [City 0, City 1, City 3]
  City 3 -> [City 1, City 2]
  Cities 0 and 3 have 2 neighboring cities at a distanceThreshold = 4, but we have to return city 3 since it has the greatest number.

Example 2:

• Input: n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
• Output: 0
• Explanation: The figure above describes the graph.
  The neighboring cities at a distanceThreshold = 2 for each city are:
  City 0 -> [City 1]
  City 1 -> [City 0, City 4]
  City 2 -> [City 3, City 4]
  City 3 -> [City 2, City 4]
  City 4 -> [City 1, City 2, City 3]
  The city 0 has 1 neighboring city at a distanceThreshold = 2.

Constraints:

• 2 <= n <= 100
• 1 <= edges.length <= n * (n - 1) / 2
• edges[i].length == 3
• 0 <= fromi < toi < n
• 1 <= weighti, distanceThreshold <= 10^4
• All pairs (fromi, toi) are distinct.

Hint:

1. Use Floyd-Warshall's algorithm to compute any-point to any-point distances. (Or can also do Dijkstra from every node due to the weights are non-negative).
2. For each city calculate the number of reachable cities within the threshold, then search for the optimal city.

[mah-shamim]

To solve this problem, we can follow these steps:

1. Initialize the Distance Matrix: Create a distance matrix dist where dist[i][j] represents the shortest distance between city i and city j. Initialize the matrix with INF (a large number representing infinity) and set dist[i][i] to 0 for all i.

2. Populate the Distance Matrix with Given Edges: Set the distances based on the given edges.

3. Floyd-Warshall Algorithm: Update the distance matrix using the Floyd-Warshall algorithm to find the shortest paths between all pairs of cities.

4. Calculate Reachable Cities: For each city, count the number of cities that can be reached within the distanceThreshold.

5. Find the Desired City: Identify the city with the smallest number of reachable cities. If there are multiple such cities, return the one with the greatest number.

Let's implement this solution in PHP: 1334. Find the City With the Smallest Number of Neighbors at a Threshold Distance

<?PHP
// Example usage:
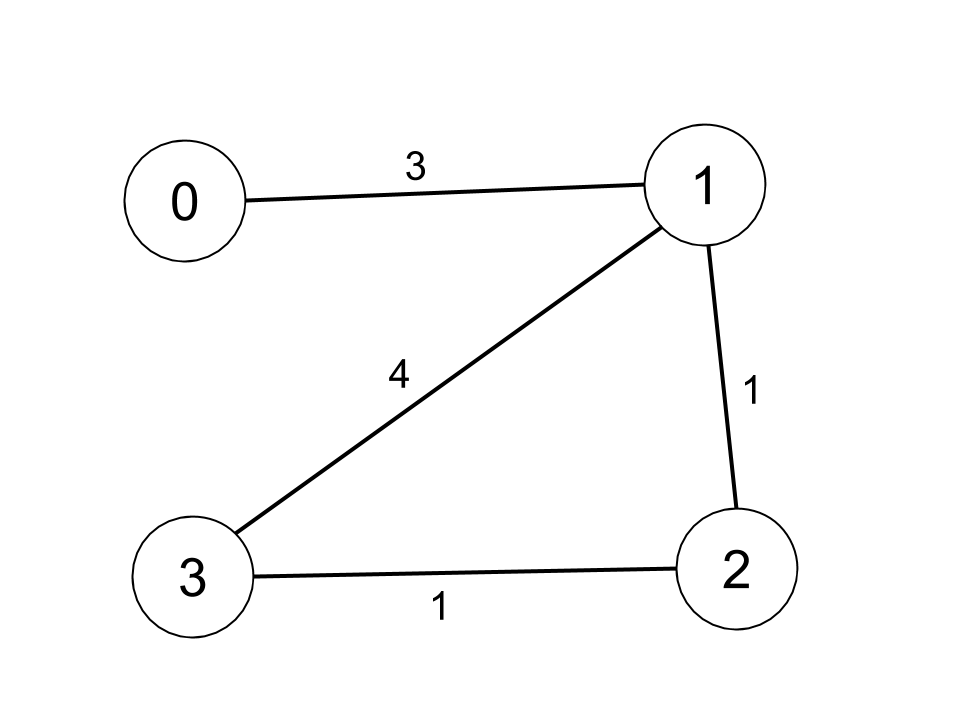
$n1 = 4;
$edges1 = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]];
$distanceThreshold1 = 4;
echo findTheCity($n1, $edges1, $distanceThreshold1); // Output: 3

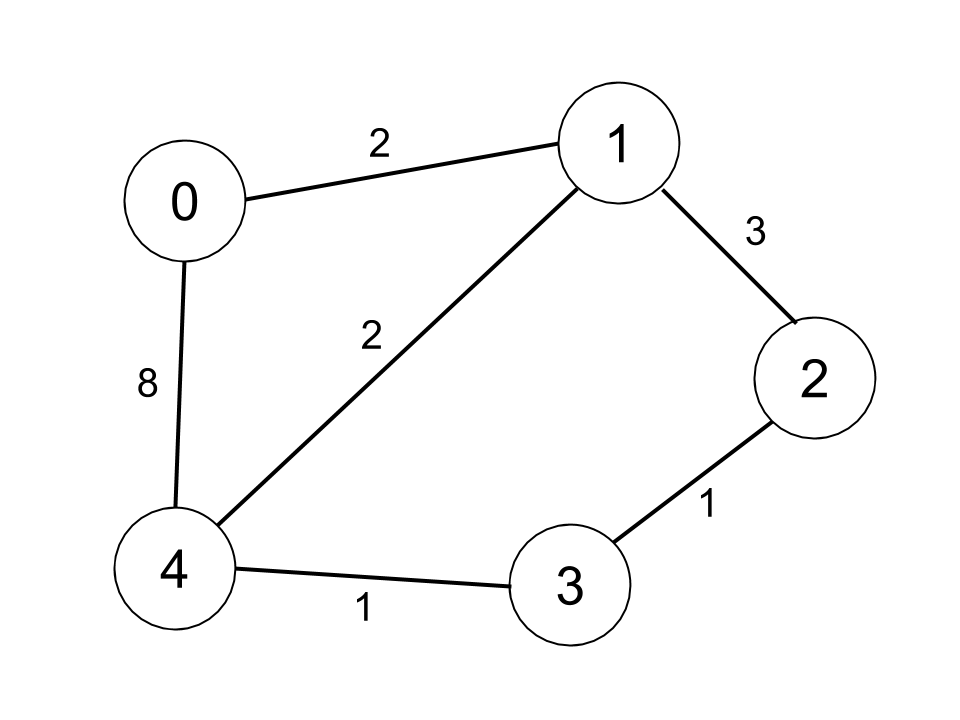
$n2 = 5;
$edges2 = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]];
$distanceThreshold2 = 2;
echo findTheCity($n2, $edges2, $distanceThreshold2); // Output: 0

?>

This code solves the problem by using the Floyd-Warshall algorithm to compute the shortest paths between all pairs of cities and then counts the number of reachable cities within the given distance threshold for each city. Finally, it returns the city with the smallest number of reachable cities, breaking ties by choosing the city with the greater number.